优先队列

Posted on | In | Visitors:

Cousera 《Algorithms I》课程作业，对优先队列的应用的几个小问题。

本文参考keyvanakbary,ForeseeMark,zerods-seu的成果

  1. 8 puzzle
  2. Dynamic Median
  3. RandomizedPQ
  4. Taxicab

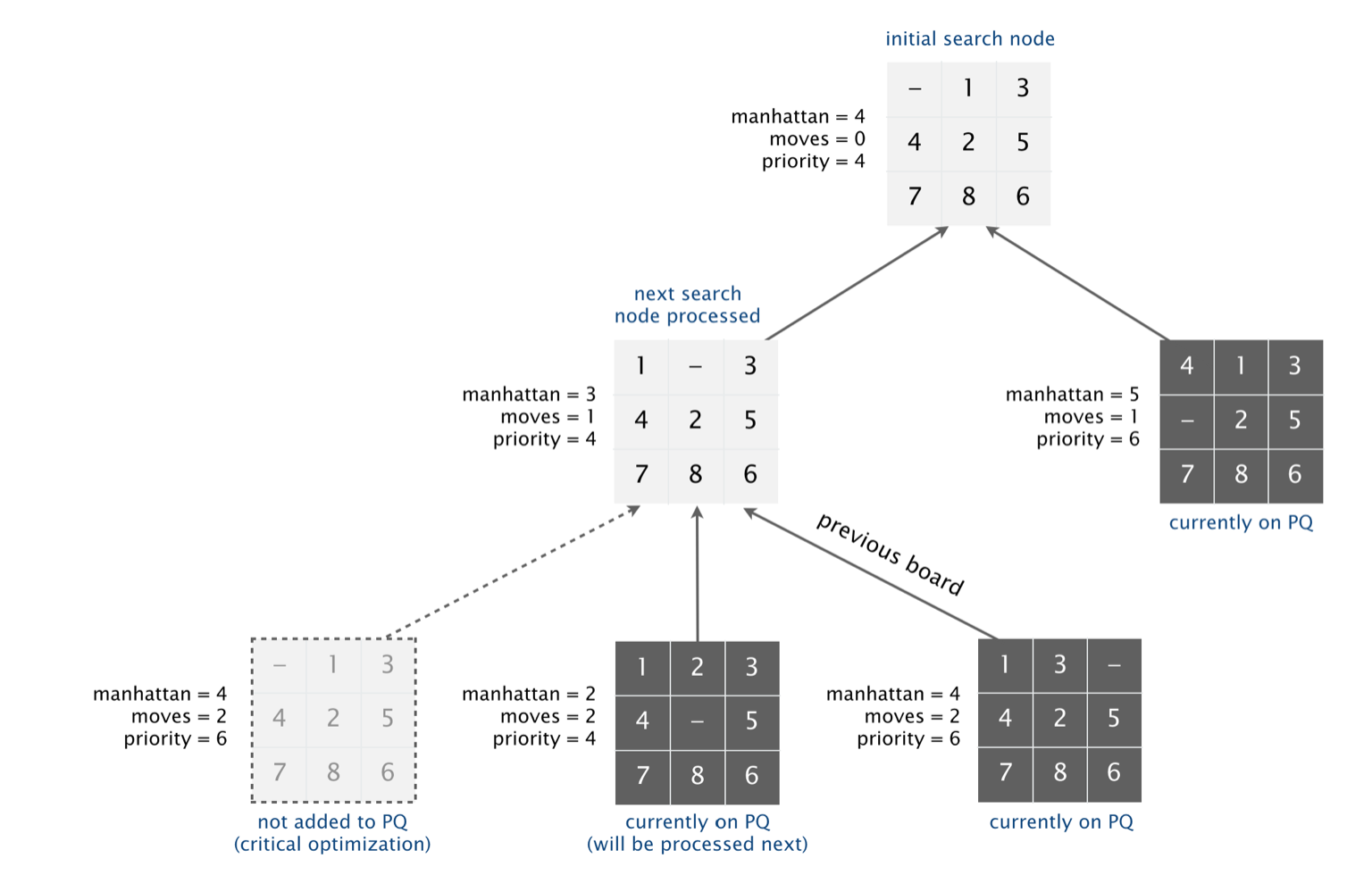
1、8 puzzle

类似于华容道，A*算法的应用,对于 Dijstra 来说省略无用的路径，更加高效。

由两个类构成 Board() & Soler()， 相当于以版做单位， 移动之后的状态作为新的 Board，存储于优先队列中。

1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
import java.util.LinkedList;

/** Week 4 - 8 puzzle
 * Reference: keyvanakbary
 * Url: https://github.com/keyvanakbary/princeton-algorithms/blob/master/week-4-8-puzzle
 */
public class Board {
    private static int[][] blocks;

    public Board(int[][] blocks) { //immutable data type
        this.blocks = copy(blocks);
    }

    private int[][] copy(int[][] blocks) {
        int[][] copy = new int[blocks.length][blocks.length];
        for (int row = 0; row < blocks.length; row++)
            for (int col = 0; col < blocks.length; col++)
                copy[row][col] = blocks[row][col];

        return copy;
    }

    public int dimension() {
        return blocks.length;
    }

    /**
     * Number of blocks out of place
     * @return count
     */
    public int hamming() {
        int count = 0;
        for (int row = 0; row < dimension(); row++) {
            for (int col = 0; col < dimension(); col++) {
                if (blocks[row][col] == 0) continue;
                if (blocks[row][col] != row * dimension() + col + 1)
                    count++;
            }
        }
        return count;
    }

    /**
     * sum of Manhattan distances between blocks and goal
     * @return sum
     */
    public int manhattan() {
        int sum = 0;
        int r, c;
        for (int row = 0; row < dimension(); row++) {
            for (int col = 0; col < dimension(); col++) {
                if (blocks[row][col] == 0) continue;
                r = (blocks[row][col] - 1) / dimension();
                c = (blocks[row][col] - 1) % dimension();
                sum += (Math.abs(row - r) + Math.abs(col - c));
            }
        }
        return sum;
    }

    public boolean isGoal() {
        for (int row = 0; row < dimension(); row++) {
            for (int col = 0; col < dimension(); col++) {
                if (blocks[row][col] == 0) continue;
                if (blocks[row][col] != row * dimension() + col + 1) return false;
            }
        }
        return true;
    }

    /**
     * Judging whether a Board is solvable with a twin Board
     * @return twin Board
     */
    public Board twin() {
        int[][] copy = copy(blocks);
        int rr = 0;
        if (blocks[rr][0] * blocks[rr][1] == 0) rr = 1;
        copy[rr][0] = blocks[rr][1];
        copy[rr][1] = blocks[rr][0];
        return new Board(copy);
    }

    public boolean equals(Object that) { // instanceof 指出对象是否是特定类的一个实例
        if (this == that) return true;
        if (that == null || !(that instanceof Board)
                || ((Board) that).blocks.length != blocks.length) return false;
        for (int row = 0; row < dimension(); row++)
            for (int col = 0; col < dimension(); col++)
                if (((Board) that).blocks[row][col] != blocks[row][col]) return false;
        return true;
    }

    /**
     * Add the available neighbors to the priority queue
     * @return an Iterable LinkedList<Board>
     */
    public Iterable<Board> neighbors() {
        LinkedList<Board> neighbors = new LinkedList<>();

        int sR= SpaceLocation()[0];
        int sC = SpaceLocation()[1];

        if (sR > 0) neighbors.add(new Board(swap(sR, sC, sR - 1, sC)));
        if (sR < dimension() - 1) neighbors.add(new Board(swap(sR, sC, sR + 1, sC)));
        if (sC > 0) neighbors.add(new Board(swap(sR, sC, sR, sC - 1)));
        if (sC < dimension() - 1) neighbors.add(new Board(swap(sR, sC, sR, sC + 1)));

        return neighbors;
    }

    /**
     * Swap two blocks
     * @param r1 row of block1
     * @param c1 col of block1
     * @param r2 row of block2
     * @param c2 col of block2
     * @return the swapped array
     */
    private int[][] swap(int r1, int c1, int r2, int c2) {
        int[][] sblocks = copy(blocks);
        int tmp = sblocks[r1][c1];
        sblocks[r1][c1] = sblocks[r2][c2];
        sblocks[r2][c2] = tmp;

        return sblocks;
    }

    /**
     * @return an array with the location of Space
     */
    private int[] SpaceLocation() {
        int flag = 0;
        int[] SL = new int[2];
        for (int row = 0; row < dimension(); row++) {
            for (int col = 0; col < dimension(); col++) {
                if (blocks[row][col] == 0) {
                    SL[0] = row;
                    SL[1] = col;
                    flag = 1;
                    break;
                }
            }
            if (flag != 0) break;
        }
        return SL;
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(dimension() + "\n");
        for (int i = 0; i < dimension(); i++) {
            for (int j = 0; j < dimension(); j++) {
                s.append(String.format("%2d ", blocks[i][j]));
            }
            s.append("\n");
        }
        return s.toString();
    }

}

2、Dynamic Medianjjjoo,

找到一组数的中位数

（1）增加一个元素，时间 O(log(n))时间

（2）返回当前元素集合的中位数，O(n)时间。

（3）删除中位数，log(n)时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
import edu.princeton.cs.algs4.MaxPQ;
import edu.princeton.cs.algs4.MinPQ;

/** ********************************************************************************
 * Week4: Interview Questions: Priority Queues
 *  Dynamic Median
 *  使用两个堆维护中位数，这里临界条件"="在MaxPQ上
 *  judge() 存在边界bug
 *  Reference：1 ForeseeMark https://blog.csdn.net/wr339988/article/details/55813202
 *             2 zerods-seu  https://blog.csdn.net/zerodshei/article/details/54346425
 ***********************************************************************************/

public class DynamicMedian {
    private MinPQ minPQ = new MinPQ();
    private MaxPQ maxPQ = new MaxPQ();
    public int num = 0;

    public DynamicMedian() {}

    public void insert(int n) {
        if (num == 0) {
            minPQ.insert(n);
            num++;
            return;
        }
        if (num == 1) {
            maxPQ.insert(n);
            num++;
            return;
        }

        if (n <= (int) maxPQ.max()) maxPQ.insert(n);
        else minPQ.insert(n);

        judge();
        num++;
    }

    public int nums() {
        return num;
    }

    public void delMid() {
        judge();
        maxPQ.delMax();
        num--;
    }

    /** ****************************************************************************
     * 2018-09-30
     * 判断: 若两个堆的元素个数>1, 则将大堆的顶部元素放入小堆中重排
     * 【2】中直接以大堆的顶部元素作为中位数，可能会出现边界情况：[2,3,1]
     *  delMid() 返回 3 ------- BUG
     *
     *      minPQ   maxPQ
     *        2       3
     *              1
     * 2018-10-09 update
     * +立flag 解决边界调节的bug
     *******************************************************************************/
    private void judge() {
        if (num == 0) throw new NullPointerException();
        boolean flag = false;
        int subVal = maxPQ.size() - minPQ.size();
        while (Math.abs(subVal) >= 1) {
            if (subVal == 1 && flag) break;
            if (subVal < -1) maxPQ.insert(minPQ.delMin());
            if (subVal == -1) {
                maxPQ.insert(minPQ.delMin());
                flag = true;
            }
            if (subVal > 1) minPQ.insert(maxPQ.delMax());
            subVal = maxPQ.size() - minPQ.size();
        }
    }

    public int queryMid() {
        return (int) maxPQ.max();
    }

    // Test
    public static void main(String[] args) {
        DynamicMedian dm = new DynamicMedian();
        dm.insert(4);
        dm.insert(3);
        dm.insert(5);
        System.out.println(dm.queryMid());
        dm.delMid();
        dm.insert(10);
        dm.insert(2);
        System.out.println(dm.queryMid());
    }
}

3、RandomizedPQ

具体和课程中给出的优先队列并无二致，加入 delRandom()随机删除一个元素，和删除堆顶元素类似

1
2
3
4
5
6
7
8
9
10
11
public Key delRandom() {
    if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
    int rdNum = StdRandom.uniform(1,n);
    Key rd = pq[rdNum];
    exch(rdNum, n--);
    sink(rdNum);
    pq[n+1] = null;     // to avoid loiterig and help with garbage collection
    if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2);
    assert isMinHeap();
    return rd;
  }

4、Taxicab

Taxicab numbers. A taxicab number is an integer that can be expressed as the sum of two cubes of integers in two different ways: a3+b3=c3+d3. For example, 1729=93+103=13+123. Design an algorithm to find all taxicab numbers with a, b, c, and d less than n.
Version 1: Use time proportional to n2logn and space proportional to n2.
Version 2: Use time proportional to n2logn and space proportional to n.

zerods-seu的文章中写到：先计算出所有小于 n1/3 +1 的整数的 3 次方，放在数组 cube[]里面，然后循环，从余下项目中二分法查找(obj-num2), 如果找到了 count++，最后如果 count 等于 2, 那么既满足要求。复杂度是$n4/3logn 的，空间复杂度是 n1/3+1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

import edu.princeton.cs.algs4.StdOut;

import java.util.*;
public class Taxicab {

    public boolean find(int a) {
        int count = 0;
        int cbrt = (int) Math.cbrt(a);   // 小于等于该数字的立方根
        for (int i = 1; i <= cbrt; i++) {

            int diff = a - (i * i * i);
            int a1 = (int) Math.cbrt(diff);
            if (a1 == Math.cbrt(diff)) count++;
            if (count > 2) return true;
        }
        return false;
    }

    public int[] Numb(int a) {
        int count = 0;
        int[] nums = new int[4];
        int cbrt = (int) Math.cbrt(a);   // 小于等于该数字的立方根
        for (int i = 1; i <= cbrt; i++) {
            int diff = a - (i * i * i);
            int a1 = (int) Math.cbrt(diff);
            if (a1 == Math.cbrt(diff)) {
                count++;
                if (count == 1) {
                    nums[0] = i;
                    nums[1] = a1;
                }
                if (count == 2) {
                    nums[2] = i;
                    nums[3] = a1;
                }
            }
            if (count > 2) return nums;
        }
        return null;
    }

    public static void main(String[] args) throws Exception {
        Taxicab tc = new Taxicab();
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int i = 0, k = 1;
        while (i < n) {
            if (tc.find(k)) {
                i++;
                System.out.println(i + " th ramanujan number is " + k);
                System.out.println(tc.Numb(k)[0] + " " + tc.Numb(k)[1]
                        + " & " + tc.Numb(k)[2] + " " + tc.Numb(k)[3]);
            }
            k++;
        }
        scan.close();
    }
}